​「深度解析」多元函数极限，你了解多少？

「深度解析」多元函数极限，你了解多少？

多元函数极限是高等数学中的一个基本概念，它涉及多个自变量的函数在某一点或者沿着某条路径的逼近行为。多元函数通常表示为 f(x, y) 、 f(x, y, z) 等，其中 ( x, y, z ) 是独立的变量。

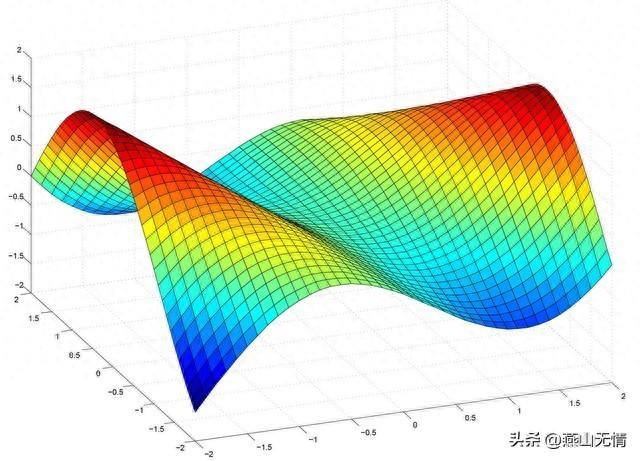
考虑一个定义在平面区域 D 上的二元函数 f(x, y) ，多元函数极限关注的是当 (x, y) 趋近于某一临界点，比如说点 (a, b) ，函数值 f(x, y) 的趋势。这种极限分为以下几种情形：

1. 沿着不同方向趋近的极限可能不同：这意味着当 (x, y) 沿不同路径趋近于点 (a, b) 时，函数 f(x, y) 的极限可能不相同。

2. 连续性与极限的关系：如果函数 f(x, y) 在点 (a, b) 附近连续，则它在点 (a, b) 处的极限存在，并且等于函数在该点的值。这是多元函数连续性的必要条件之一。

3. 偏导数与极限的关系：如果函数 f(x, y) 在点 (a, b) 处的各个偏导数都存在，那么可以认为函数在该点附近的行为是由偏导数决定的。然而，偏导数的 existence 并不保证极限的存在性。

4. 极坐标下的极限：在处理圆周或者极点附近的问题时，使用极坐标 (r, \theta) ) 可能会更加方便。在这种情况下，极限问题转化为 r 趋近于某个值（可能是 0 或正无穷）时，函数的行为。

为了判断多元函数在某点的极限是否存在，常用的方法包括：

- 直接代入法：尝试将趋近的点直接代入函数表达式，看是否能够得到确定的结果。

- 参数方程法：如果函数可以通过参数方程来描述，可以尝试通过改变参数来研究极限。

- 分部讨论法：对于复杂函数，可能需要分别考虑不同的趋近路径或者方向。

- 极坐标法：对于涉及圆形或周期性结构的问题，使用极坐标可能更为直观。

在研究多元函数极限的过程中，经常会遇到一些特殊情形，如“不连续点”、“奇异点”等，这些都需要特别的注意和技巧去分析和求解。此外，多元函数极限的概念还可以拓展到更高维度，比如三元、四元函数，甚至是函数序列和函数项级数的研究中。